【續_解出】正方體展開圖體積的最大值?!【南一數學國際題】

繼續正方體展開圖體積的最大值問題，有方法可以解決。

   解決方法如下，需假設一些參數，然後藉由亂來三明治(夾擠)定理、投射來計算，

   就是用真實角度α，進而將增長的長方形旋轉，其邊長投射在X、Y軸上，限制不能超過長方形紙板的邊界(x=60,y=50)，夾擠後找到增長部分，進而找到正方形邊長，並計算出正方體體積，當然還是需要excel 來做演算的工具，以示公信力。

   下圖是假設多增加X公分，右邊是假設旋轉α，並列出所有α度數的地方。

    

  

下圖可以知道(A+B)長<60，(C+D)長<50，這就是亂來三明治定理(跟微積分一點都不像)

     

   經過邊長X=(1，2，3，2.4)cm，分別運算帶入後，可以得到下面結果。

  

(一)邊長再加1公分，長方形旋轉角度可在52∘~58∘範圍內(體積3546.57813立方公分)

 

(二) 邊長再加2公分，長方形旋轉角度可在53∘~55∘範圍內(體積3723.875立方公分)

(三)邊長再加3公分，長方形會無法旋轉，這就是夾擠的意思，這就是說增加邊長無法到3公分，所以要去找加上2公分多。 (體積3906.984375立方公分)

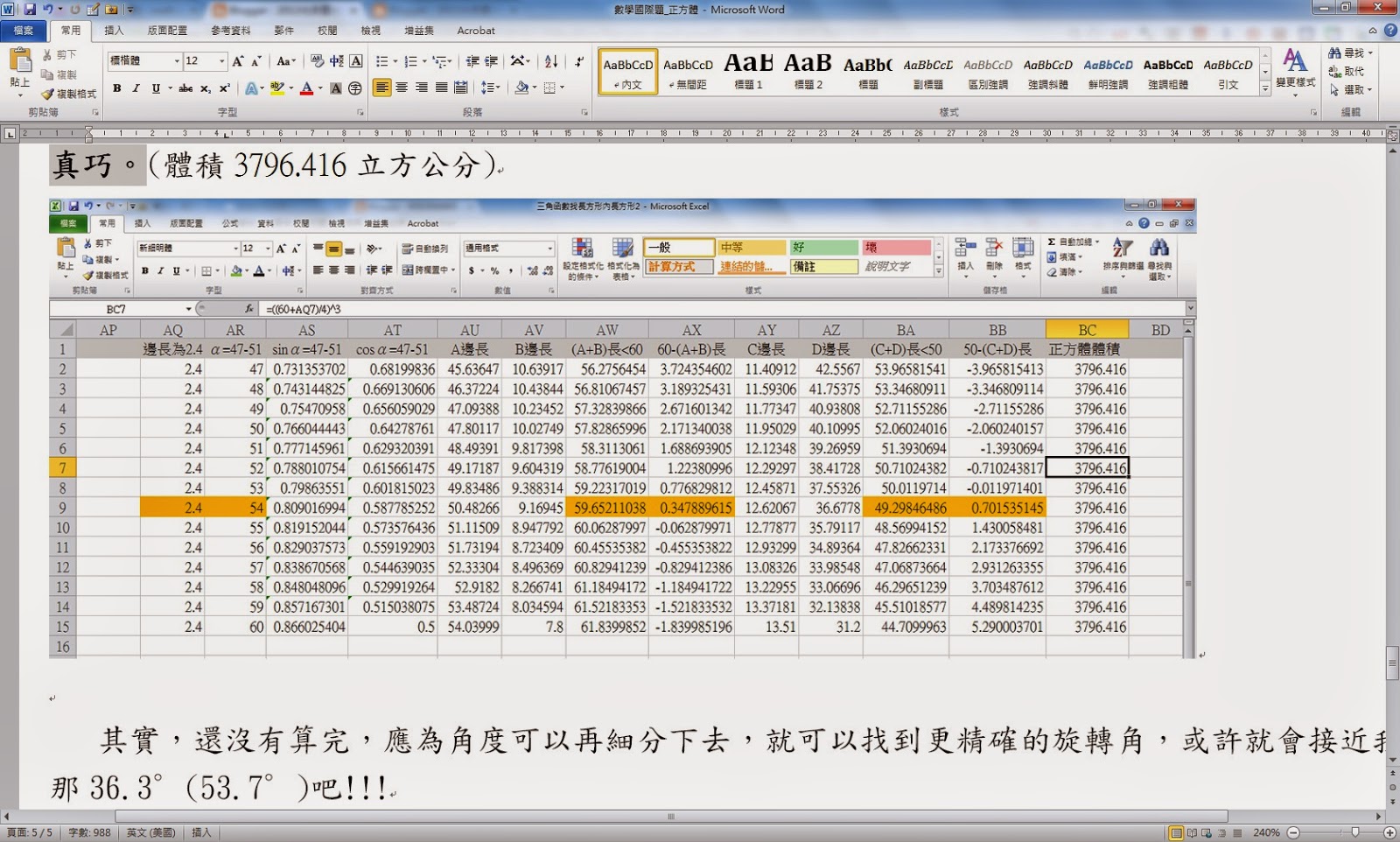
(四) 邊長再加2.4公分，長方形旋轉角度可在54∘，跟上篇推論的幾乎吻合，這次說的54∘與上次36.3∘(90-54=36)，是假設角度的差別而已，(60+2.4)/4=15.6cm，也是與上次一樣，體積也是，真巧。(體積3796.416立方公分)

 

   

   其實，還沒有算完，應為角度可以再細分下去，就可以找到更精確的旋轉角，或許就會接近我那36.3∘(53.7∘)吧!!!